
タイトルは・・・
分数のわり算はなぜ逆数をかけるのか?
なのですが、みなさんが思っているような内容ではないかもしれません。
一部の学校の先生が、インターネットか何かで知ったことを、嬉々として生徒さんたちに押し付けている事例をたまに聞きます。
あまりそれは意味ないよ、という内容です。
個人批判になってしまわないように注意します。
【分数のわり算で、逆数にしてかけ算にすることの説明法について】
一部の学校で、

のような途中式をはさむことを強いる学校の先生がいると聞きました。
何をやっているんだと不安に思う親御さんも多いでしょうから(それがふつうです)、何をやっているのか、私が代わりに説明します。
使っているのはわり算のきまりです。
「わられる数」と「わる数」を、同じ数をかけたり、同じ数で割っても商は変わらないというものです。
よい例で示しましょう。
「14÷20」
このまま計算してもそれほどたいへんではありませんが、わる数が簡単な数だと計算がより正確になります。この計算もわる数が20でなく2だったら、むずかしくとも何ともありません。20は10でわったら2になります。わられる数とわる数の両方を10でわってみましょう…
14÷20=(14÷10)÷(20÷10)=1.4÷2
あとは、1.4を半分にするだけなので、0.7が答えになります。
もう1例みてみましょう。こちらもよい例です。
「14÷0.2」
0.2が2だったらなんでもない問題ですよね。0.2は10をかければ2になります。わられる数とわる数に、それぞれ10をかけてみましょう。
14÷0.2=(14×10)÷(0.2×10)=140÷2
あとは何でもないですよね。140を半分にして70です。
最初のわり算の問題にもどります。
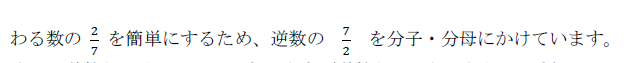
わる数が逆数をかけるので1になります(逆数とはそういうものです)。
「÷1」は無視していいので、結果としてわられる数にわる数の逆数をかけていることになります。
でも、これどうでしょうか?
確かに、「わる数をなるべく簡単にする」というのは原則ですしその原則に基づいているので、どこで知ったのかはわかりませんが、ひどく悪い考え方だとはいえないでしょう。
ただし、よくもないですよね。なんせ最初の( )だけで答えです。
算数できる子はスルーして、できない子は混乱するだけでしょう。
形だけ解法に当てはめていることに変わりはありません。
(厳密にいうと、これは「わる数を逆数にしてかけて計算すればいい」ことの証明であり、「わる数を逆数にしてかける」ことの説明にはなっていません。)
いえ、言い換えます。よくなくないこともないですが、無理強いするまでもないだろう、というのが正確ですね。(それほどすごくもありません。ここでどうこう言うくらいなら、先ほどの小数のわり算の工夫を定着させる方が有効でしょうね。)
私の考えを言います。
分数のわり算をつかむためには、(分数)÷(整数)の段階で、逆数という考え方を持ち込まずに、分数を割るということはどういうことか、しっかりつかむことにあります。
日本の算数カリキュラムは、「時間」を重視しています。
具体的に言いますと、小学5年生で(分数)÷(整数)を習い、それを十分熟成させてから6年生で(分数)÷(分数)を勉強します。
6年生でも(分数)÷(整数)を定期的に確認するのが有効でしょう。
本当は、もっと言いたいこともありますがこの程度にしておきます。
その先生が、他の単元をどのように説明しているかがポイントですね。
シェア歓迎します。リンクもフリーです。